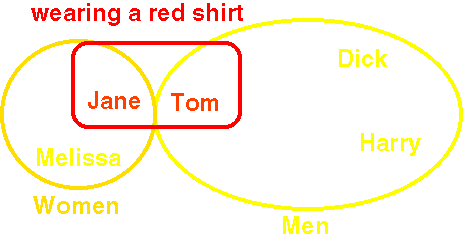
Objects classified by shared attributes.
All members belong equally.
NOTE: Examples based on a footrace. "Objects" in this case are people.
[Critique of traditional categories]
abbreviated intellectual history
developed in physics (and related sciences) by late 19th century
numerical relationship between standard& object measured;
inherent in object
Example: US
Office of Weights and Measures | standard
kilogram | Legal
Weights and Measures in the State of Indiana
[still a tacit part of geographic databases?]
Bertand Russell; Campbell; Bridgeman; Stevens ...
properties not inherent in object; numbers derive from measurement
operations
20th century dominated by representationalists.
Measurement theorists concentrated on physics
'extensive' measures (eg. length) emphasized strict limits; special
role for addition
'Operationism' enshrines the procedure;
result: no room for social sciences
Stevens: a psychophysicist
research on perceived loudness of sound
measurements rejected by operationists
General movement for quantitative approach to social sciences
Published 1946 in Science (without any references)
Adopts 'nominalist' form of representationalism:
Defines measurement as 'assignment of numbers to objects according
to a rule'
Measurement scale defined by properties of numbers (not properties
of the rules or objects)
Scales organized by transformations under which the meaning remains
invariant.
1946: Nominal, Ordinal, Interval, Ratio
(log-interval added in 1959)
Links scales to permissible statistics
Scale Empirical Invariance Permissible
Operations Group Statistics
NOMINAL equality any 1:1 substitution Mode
Number of cases
ORDINAL , > any monotonic Median
function Percentiles
INTERVAL equality of x' = ax + b Mean, std. dev.
intervals Correlations
RATIO equality of x' = ax Coefficient of
ratios variation

Objects classified by shared attributes.
All members belong equally.
NOTE: Examples based on a footrace. "Objects" in
this case are people.
[Critique of traditional categories]
Order of arrival of contestants in footrace
Women's race Men's race
First Jane Tom
Second Melissa Dick
Third Leila Harry
...
Ordinal measures may be complete orderings, partial orderings
or ranked categories
(High, Medium, Low)
(slight, medium, severe, very severe limitations)
Examples: Grading
Sweet Potato crops in Indiana | Plant
Hardiness in Texas
 Interval
measures require a fixed distance, but the zero point is arbitrary.
Interval
measures require a fixed distance, but the zero point is arbitrary.
Differences between two interval measures are ratio.
Interval measures are often raw results, with some additional
relationships they become ratio.
A frequent example of interval measurement is temperature in
degrees F, or °C.
The 'interval' equation does apply:
degrees F = ( 5/9 · degrees C ) + 32
BUT degrees K is not the 'true' ratio scale (extensive).
To combine regular extensive measures: ADD
To combine temperatures:
Two objects brought in contact reach a weighted equilibrium temperature.
Current Local Weather data:
(Use BACK to return)
 Ratio measures
have:
Ratio measures
have:
a fixed zero that means 'no quantity';
a constant interval (distance on the scale).
May be rescaled because '1' is arbitrary.
Examples of ratio scales: SI
units | Physical
Reference Data (CODATA 86) | Bushels
in Indiana
Stevens conflated two types of ratio measures.
Extensive: based on addition rule for combination
examples: distance, mass, time
Derived: created by division of extensive measures;
velocity = distance / time (speed
of light meters per second) , Newtonian
constant of gravitation, etc.
Different axioms apply
(recognized in thematic cartography practice)

Extensive: proportional symbols
Derived: choropleth [See Figure 1-8 and 1-9 in Exploring GIS]
In 1959, Stevens recognizes that the invariance rules could
allow another scale on the same 'level' as interval.
The invariance function would have the form: x' = a times x to
the b power
This 'log-interval' scale is mostly theoretical, though earthquake
intensities on Richter and Mercali scales use this form.
None of the social science statistics textbooks take notice; cartographers
still use the basic 4.
Ratio is not the 'highest' level of measurement, '1' need not
be arbitrary.
Using Stevens' invariance scheme, an 'absolute' scale could
not be rescaled by any multipier.
Both zero AND one are fixed.
Probability is an absolute scale.
Bayes' Law and other axioms depend on absolute scaling.
Just as a difference of intervals is ratio, some divisions of
ratios produce absolute measures.
Some measures are obtained by tabulating the total of some objects inside a larger collecting unit.
Are counts higher than ratio?
Are counts 'discrete' like categorical measures?
One answer: Counts are counts;
Extend the system to handle all the cases.
Stevens scales only accomodate open-ended linear scales.
Some measures are cyclical, with a fixed range.
Example: Angles
Additional axioms are required to handle the fact that 359° is the same distance from 0° as 1° is.
Multidimensional scales have extra relationships.
In Stevens' scheme, an unbounded linear axis could not be fit
into a fixed interval without losing information.
yet, two unbounded Cartesian axes can be transformed into
radial coordinates with only one unbounded axis, and one angle.

Physics Devices at Cornell <Dead? too bad>
'Nominal' measures depend upon Aristotle's view:
categories imply shared values of attributes.
Hence, test for equivalence only.
Two alternative approaches to categories:
Both provide a metric for membership beyond the simple Yes/No of traditional categories.
Matthews Datasets | Fish and Wildlife Service "Cowardin" manual for wetland classification (and its official hierarchy); National list of plants associated with wetlands (1996) with 5 categories of association <now dead> | FGDC Vegetation Standard <relocated?>|
The four levels are not adequate.
New Requirements:
Measurement involves more axioms than just those involved in the number line.
Stevens never questions the nature of the 'object'.
[in psychology, the 'case' is not a problem]
Standard model: case 'has' attributes
(not relationships that can be measured)
Geographical Matrix: places 'have' attributes
'Case' permits measurement as a form of control.
Geographic control is not completely routine and accepted.
Scheme based on Sinton: fixed, controlled, measured
Object Control Isolated objects: 'features'; isolines Connected objects: network; coverage Spatial Control Point-based: center point Area-based: (many rules) Relationship Control Triangular Irregular Network (TIN) Composite Frameworks (eg. Choropleth)
basic rules: attribute serves as control, positions measured to suit