What is this course about anyway?

Integration of information from different sources

Objectives

Provide review of course material
Refine learning objectives
Present course in simplified form

Materials:

List of terms, Glossary of book, Worksheet on Measurement frameworks, Worksheets on measurement and reference systems (.doc), Original form of Objectives,

The key trick of a GIS is integrating information from diverse sources. The tough steps are when the integration is not predetermined, but must be discovered from information usually taken for granted.

In labs, we have used a raster solution in ArcMap Spatial Analyst: Integration performed by imposing common set of spatial objects. We have also used vector methods, integration by finding a common geometry.

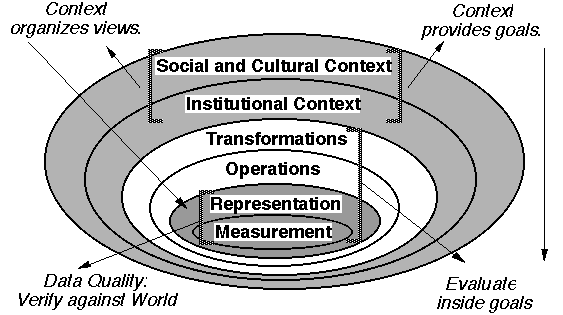
Review rings of ever increasing complexity (scope) provided at start of course:

Integrate different Levels of Measurement

"Everything is a number" fallacy

How to balance a need to choose with diverse characteristics that do not support the simple arithmetic of continuous measures. (weighting and rating)
Learning to live with categories and what you can do with them. Basic set theory expanded to handle less rigid rules
Nuances beyond Stevens: for example, totals are different from classical ratio measures

Integrate different measurement frameworks

Choice of control: Space controlled/ attribute measured NOT EQUIVALENT TO attribute controlled/ space measured
Grid coding rules are a form of control: point vs. area; space vs attribute
Thinking through to the axioms (assumptions) behind the measurements

Integrate by connecting transformed distributions

Geometric conversions - Buffers as geometric constructions; other neighborhoods
Transform between frameworks: attribute assumptions; neighborhood construction

Integrate different attitudes towards error (risk)

tradeoff between spatial and attribute resolution/ accuracy
SCALE (and all the decisions subsumed therein)

Integrate different spatial reference frameworks

actually raster forces this to be done externally, but it still occurs.

Integrate different institutional arrangements
Making organizations with distinct goals cooperate; share a more complex world view

Integrate different cultural frameworks

Making societies (cultures) with distinct goals cooperate; share a common language

LESSONS:
Mathematics can help. Theoretical framework for measurement can develop an outer bounds on what seem to be difficult problems.

Mathematics are not enough. Integration of information involves meaning. Models are not universal, but must be rooted in the substantive problem.